| 入試問題解説:灘中学の解説(平成18年) |
| 《 第 1 日 》 |
| 【6】 |
もとの数を35で割った余り(0〜34)をa、40で割った余り(0〜39)をbとすると次の左図のように表せる。この時、もとの数は長方形の面積となり、その面積は上下で同じである。
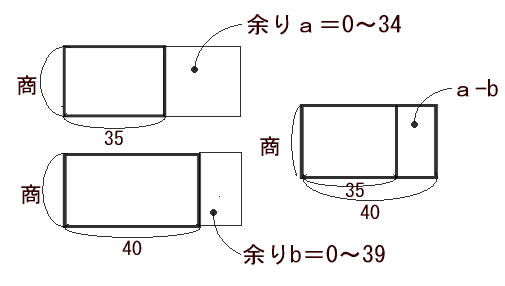
左図の太線の長方形を重ね合わせると右図となる。
余りの差aーbは40−35=5より5の倍数となる。
aーbが0から34の範囲となり、もとの数が3桁より商は2以上となる。
したがってaーbは10,15,20,25,30の可能性がある。
つまり商は2,3,4,5,6となる。
(1)商=2の時(aーb=10)
aは10から34の可能性があるので、
もとの数は35×2+10〜35×2+34となり、80〜104となる。
もとの数は3桁より、100〜104の5個となる。
(2)商=3の時(aーb=15)
aは15から34の可能性があるので、
もとの数は35×3+15〜35×3+34となり、120〜139の20個となる。
(3)商=4の時(aーb=20)
aは20から34の可能性があるので、
もとの数は35×4+20〜35×4+34となり、160〜174の15個となる。
(4)商=5の時(aーb=25)
aは25から34の可能性があるので、
もとの数は35×5+25〜35×5+34となり、200〜209の10個となる。
(5)商=6の時(aーb=30)
aは30から34の可能性があるので、
もとの数は35×6+30〜35×6+34となり、240〜244の5個となる。
(1)〜(5)より、もとの数は5+20+15+10+5=55個となる。
また、最大の数は244である。
|
|
|

