| ����������F�咆�w�i�����P�W�N�j |
| �s �� �P �� �t |
|
| �y�P�z�@ |
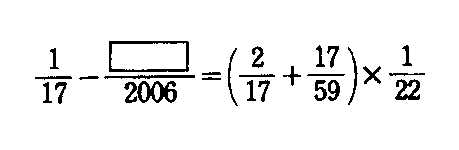 |
 |
| �y�Q�z�@�@�@ |
�S�̈قȂ鐔���P�C�R�C �C�X����R�̈قȂ鐔�������o���ĕ��ׂĂł���R�����̐����͂Q�S����A���̕��ς͂T�T�T�ł���B �C�X����R�̈قȂ鐔�������o���ĕ��ׂĂł���R�����̐����͂Q�S����A���̕��ς͂T�T�T�ł���B
|
 |
| �y�R�z�@�@�@ |
A�n�_�Ƃa�n�_�͂P�O��������Ă���B�o�N�͂`�n�_����a�n�_�֖����S�����ŕ������A�R�O�������Ă͂T���x�ނƂ������Ƃ����Ԃ��B�p�N�͖����P�Q�����ŋx�ނ��ƂȂ����]�Ԃła�n�_����`�n�_�Ő܂�Ԃ��a�n�_�Ɍ������B�o�N�C�p�N�͓����ɏo������B�p�N���`�n�_�Ő܂�Ԃ����̂��o�N��ǂ��z���̂́A�Q�l���o�����Ă��� ����ŁA���̒n�_�͂`�n�_���� ����ŁA���̒n�_�͂`�n�_���� �����̏��ł���B �����̏��ł���B
|
 |
| �y�S�z |
���w�U�N���S�O�l�ɁA����C�Z���C���Ȃɂ��āu�D���v�Ȃ���A�u���炢�v�Ȃ�~�����������Ƃ���A���̑����͂P�O�O�ŁA�~�̑����͂Q�O�ł���A�R���Ȃ��ׂĂɁ~���������k�͂��Ȃ������B�Z���Ɂ����������k�͂R�T�l�ŁA���̂����Q�l�͎Z�������Ɂ������A�Z���Ɂ~�C���ȂɁ����������k�͂S�l�ł������B���̂Ƃ��A���ꂾ���Ɂ����������k�̐l���� �l�ł���B�܂��A�R���Ȃ��ׂĂɁ����������k�̐l���͍ł������� �l�ł���B�܂��A�R���Ȃ��ׂĂɁ����������k�̐l���͍ł������� �l�ł���B �l�ł���B
|
 |
| �y�T�z�@�@�@ |
�T�����̂R�U�̔{���ŁA�Q�C�R�C�T�̂ǂ���������ꂩ�̂����ɂ�����鐮���i�Ⴆ�T�R�X�Q�W�Ȃǁj�̂����A�ł����������̂� �ł���B �ł���B
|
 |
| �y�U�z�@�@ |
�P�O�O���R�T�Ŋ���Ə��͂Q�A�]��͂R�O�ŁA�S�O�Ŋ���Ə��͂Q�A�]��͂Q�O�ł���B�R�����̐����̂����R�T�Ŋ����Ă��S�O�Ŋ����Ă����������ɂȂ���̂́A�P�O�O���܂߂đS���� ����A���̂����ł��傫�������� ����A���̂����ł��傫�������� �ł���B �ł���B
|
 |
| �y�V�z |
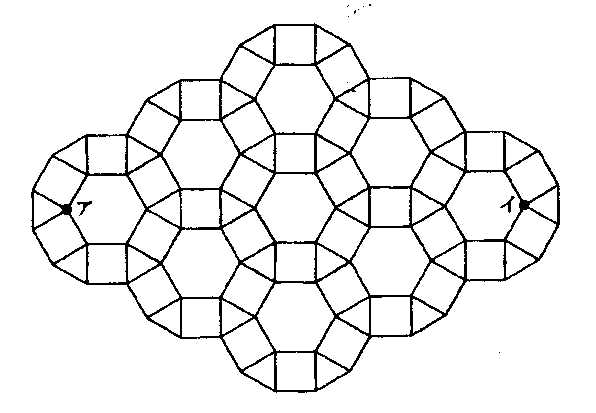
���̐}�͂P�ӂ̒������R�����̐��Z�p�`�C�����`�C���O�p�`��g�ݍ��킹�č�������̂ł���B�����̕ӂ�ʂ��āA�A����C�܂ł����Ƃ��̍ŒZ������ �����ŁA���̍ŒZ�R�[�X�͑S���� �����ŁA���̍ŒZ�R�[�X�͑S���� �ʂ�ł���B �ʂ�ł���B |
 |
 |
| �y�W�z�@�@ |
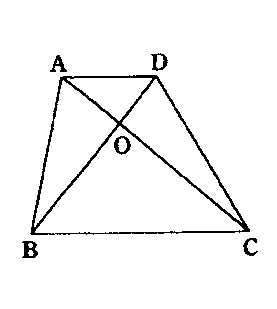
�E�̐}�̂悤�ȑ�`�`�a�b�c�ɂ����āA�_�n�͑Ίp���̍D�]�ł���B�O�p�`�`�n�a�C�O�p�`�a�n�b�̖ʐς����ꂼ��P�O���u�C�Q�T���u�ł���Ƃ��A��`�`�a�b�c�̖ʐς� ���u�ł���B ���u�ł���B |
 |
 |
| �y�X�z�@�@ |
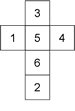
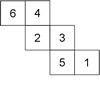
�E�̂Q�̐}�́A�e�ʂɂP����U�܂ł̐��������ꂽ�����̂̓W�J�}�ł���B���ꂼ��̗����̂̓W�J�}�ł���B���ꂼ��̗����̂̂P�̒��_�ɏW�܂�R�̖ʂɏ����ꂽ���̘a���l����B���̘a�̂����ő�̂��̂́A�}�@�ł͂P�T�A�}�A�ł� �ł���B �ł���B |
 |
�@ �@ �@  |
| �y�P�O�z |
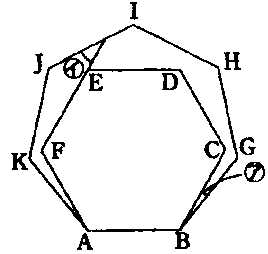
�E�̐}�̂悤�ɐ��Z�p�`�`�a�b�c�d�e�Ɛ����p�`�`�a�f�g�h�i�j������B �̊p�̑傫���� �̊p�̑傫���� �x�A �x�A �̊p�̑傫���� �̊p�̑傫���� �x�ł���B �x�ł���B |
 |
 |
| �y�P�P�z |
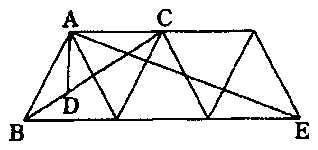
�E�̐}�͓����傫���̂T�̐��O�p�`�������ԂȂ����ׂ����̂ŁA�_�c�͂a�b�̂S�����_�̂����A�a�ɍł��߂��_�ł���B�`�d�̒������X�����̂Ƃ��A�`�c�̒����� �����ł���B �����ł���B |
 |
 |
| �y�P�Q�z |
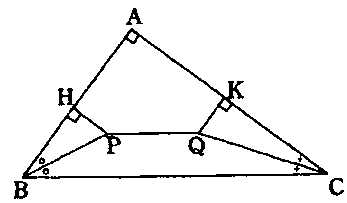
�E�̐}�̎O�p�`�`�a�b�́A�`�a�C�`�b�C�a�b�̒��������ꂼ��P�W�����C�Q�S�����C�R�O�����̒��p�O�p�`�ł���B�_�o�C�p�͂��ꂼ��p�a�C�p�b�̂Q��������̓_�ŁA�o�p�͂a�b�ɕ��s�ŁA�o�g�Ƃ`�a�A�p�j�Ƃ`�b�͂��ꂼ�ꐂ���ł���B
�܊p�`�`�g�o�p�j�̖ʐς́A�O�p�`�`�a�b�̖ʐς̔����ɂȂ��Ă���Ƃ��A�o�g�̒����� �����ŁA�o�p�̒����� �����ŁA�o�p�̒����� �����ł���B �����ł���B |
 |
 |
| �y�P�R�z |
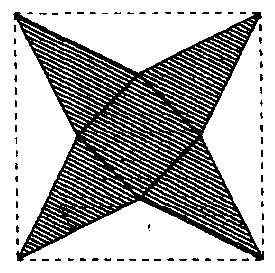
�E�̐}�̎ΐ������͂P�ӂ��W�����̐����`�����ӂ��W�����ō������Q�����̂Q���ӎO�p�`�S������Ăł������̂ł���B�����g�ݗ��ĂĂł���l�p�����̑̐ς� ����3�ł���B ����3�ł���B
�������A�p�����̑̐ς́i��ʐρj�~�i�����j���R�ŋ��߂���B |
 |
 |

